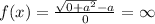Question

This is Calculus 1 Problem. Show ALL your work, giving proper context, and make sureIt is written neatly, legibly, and with appropriate organizations. MUST SHOW ALL THE JUSTIFICATION OF THE PROBLEM!!!

Answer 1

Answer:

1. The domain of the function is:

`\lbrace x\in\Re:x\\e0\text{ and }x+a^2\ge0\rbrace`

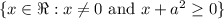
2. To define f at x = 0, we need to substitute x by 0 in the given function. The result is infinity

Step-by-step explanation:

Given the function:

`f(x)=(√(x+a^2)-a)/(x),a>0`

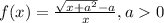
1. The domain of the function is:

`\lbrace x\in\Re:x\\e0\text{ and }x+a^2\ge0\rbrace`

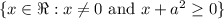
2. To define f at x = 0, we need towe need to substitute x by 0 in the given function. The result is infinity

That is;

`f(x)=(√(0+a^2)-a)/(0)=\infty`