Hello there. Given the function h(t), that is, the height of a rocket as a function of time in seconds after its launch, we have to determine the height at its vertex.
For this, we must remember some properties about finding the coordinates of the vertex of a parabola.
Given a function:
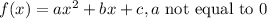
Its vertex happens at (xv, yv).
The xv-coordinate can be found by taking the arithmetic mean between the roots.
Knowing the roots are given by the quadratic formula as x1, x2:
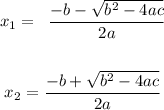
Then we have that:
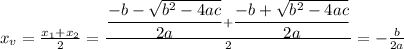
The yv-coordinate can be found by plugging xv into f:
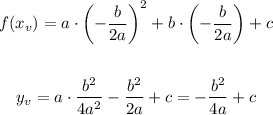
That can also be written in terms of the discriminant of the function:
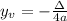
So, given the function:
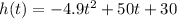
Since we want to determine the height at the vertex, then we have to determine the yv-coordinate of the function.
For this, plug a = -4.9, b = 50 and c = 30 in the formula derived earlier:
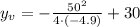
Multiply, square and add the values:
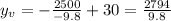
Calculating the fraction with the help of a calculator, we get
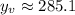
This is the maximum height reached by this rocket.
In fact, we say it is a maximum because the leading coefficient a is negative.
When it is negative, the concavity of the function is facing down, that means it admits a maximum point and it happens at its vertex. The xv coordinate gives you the time needed to reach this maximum height, while yv gives you the height;