We are given that there are 125 boxes. If "x" represents the number of larger boxes and "y" the smaller boxes then this is written mathematically as:
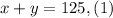
We are also given that the larger boxes weigh 45 pounds and the smaller boxes weigh 30 pounds each and the total weight is 4575 pounds. This is written mathematically as:
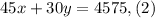
We get a system of two equations and two variables. To solve the system we will use the method of elimination. To do that we will multiply equation (1) by -45, we get:
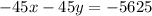
Now, we add this equation to equation (2):
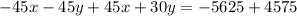
Now, we add like terms:
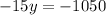
Now, we divide both sides by -15:

Solving the operations:
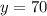
Now, we substitute the value of "y" in equation (1):
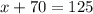
Now, we subtract 70 from both sides:
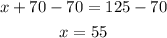
Therefore, there are 55 larger boxes and 70 smaller boxes.