Question

h is a quadratic function where h(2) = 0, h( – 5) = 0, and h(3)= - 3.12. Find an algebraic equation for h(w)

Answer 1

`h(w)=-0.39w^2\text{ -1.17b + 3}9`

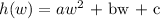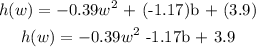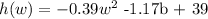
Step-by-step explanation:

Quadratic equation is in the form:

`h(x)=ax^2+bx\text{ + c }`

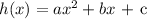
when x = 2, h(x) = 0

`\begin{gathered} 0=a(2)^2\text{ + b(2) + c} \\ 0\text{ = 4a + 2b + c} \\ \text{ 4a + 2b + c = 0 ...equation 1} \end{gathered}`

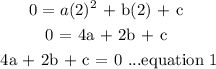
when x = - 5, h(x) = 0

`\begin{gathered} 0=a(-5)^2\text{ + b(-5) + c} \\ 0\text{ = 25a - 5b + c} \\ \text{25a - 5b + c = 0 }\ldots equation2 \end{gathered}`

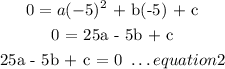
when x = 3, h(x) = -3.12

`\begin{gathered} -3.12=a(3)^2+b(3)\text{ + c} \\ -3.12\text{ = 9a + 3b +c} \\ \text{9a + 3b +c = -3.12 }\ldots\text{equation 3} \end{gathered}`

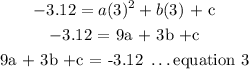
We need to find the values of a, b, c

subtract equation 2 from 1:

`\begin{gathered} 4a\text{ - 25a +2b -(-5b) +c - c = }0\text{ - 0} \\ -21a\text{ + 2b + 5b + 0 = 0} \\ -21a\text{ + 7b = 0 ..equation 4} \end{gathered}`

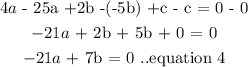
subtract equation 3 from 2:

`\begin{gathered} 25a\text{ - 9a -5b - 3b + c - c = 0 -}(-3.12) \\ 16a\text{ - 8b + 0= 0}+3.12 \\ 16a\text{ - 8b = 3.12 ...equation 5} \end{gathered}`

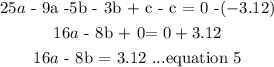
We would sove equation 4 and 5 to get a and b

Using elimination method:

multiply equation 4 by 8 and equation 5 by 7 to eliminate b

-168a + 56b = 0 ...equation 4

112a - 56b = 21.84 ...equation 5

Add both equations:

-168a +112a + 56b + (-56b) = 0+ 21.84

-56a + 56b - 56b = 21.84

-56a = 21.84

a = 21.84/-56

a = -0.39

substitute for a in any equation between 4 and 5:

112a - 56b = 21.84 ...equation 5

112(-0.39) - 56b = 21.84

-43.68 - 56b = 21.84

-56b = 43.68 + 21.84

b = 65.52/-56

b = -1.17

substittue for c in any of equation from 1-3:

25a - 5b + c = 0 ..equation 2

25(-0.39) - 5(-1.17) + c = 0

-9.75 + 5.85 + c = 0

-.39 + c = 0

c =3.9

When w = ?

h(w) = ?

replacing w with x in the formula for the quadratic above:

`h(w)=aw^2\text{ + bw + c}`
`\begin{gathered} h(w)=-0.39w^2\text{ + (-1.17)b + (3.9)} \\ h(w)=-0.39w^2\text{ -1.17b + 3}.9 \end{gathered}`