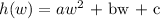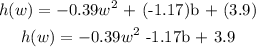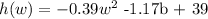
Step-by-step explanation:
Quadratic equation is in the form:
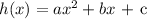
when x = 2, h(x) = 0
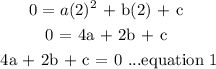
when x = - 5, h(x) = 0
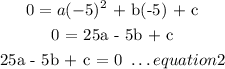
when x = 3, h(x) = -3.12
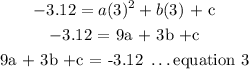
We need to find the values of a, b, c
subtract equation 2 from 1:
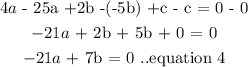
subtract equation 3 from 2:
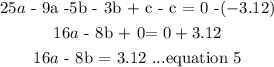
We would sove equation 4 and 5 to get a and b
Using elimination method:
multiply equation 4 by 8 and equation 5 by 7 to eliminate b
-168a + 56b = 0 ...equation 4
112a - 56b = 21.84 ...equation 5
Add both equations:
-168a +112a + 56b + (-56b) = 0+ 21.84
-56a + 56b - 56b = 21.84
-56a = 21.84
a = 21.84/-56
a = -0.39
substitute for a in any equation between 4 and 5:
112a - 56b = 21.84 ...equation 5
112(-0.39) - 56b = 21.84
-43.68 - 56b = 21.84
-56b = 43.68 + 21.84
b = 65.52/-56
b = -1.17
substittue for c in any of equation from 1-3:
25a - 5b + c = 0 ..equation 2
25(-0.39) - 5(-1.17) + c = 0
-9.75 + 5.85 + c = 0
-.39 + c = 0
c =3.9
When w = ?
h(w) = ?
replacing w with x in the formula for the quadratic above: