Question

Create a unique parabola in the pattern f(x) =( x-a)(x-b). describe the direction of the parabola and determine the y-intercept and zeros.

Answer 1

Given:

Create a unique parabola in the pattern f(x) =( x-a)(x-b).

Required:

Describe the direction of the parabola and determine the y-intercept and zeros. ​

Step-by-step explanation:

Lets first learn some concepts:

Direction of the parabola can be determined by the value of a. If a is positive, then the parabola faces up (making a u shaped). If a is negative, then the parabola faces down (upside down u).

Y-intercept:

To find the y-intercept, set x = 0 and solve for y.

Zeros:

The zeros of a function are the values of x when f(x) is equal to 0.

We have function

`f(x)=(x-a)(x-b)`
`\begin{gathered} \text{ Direction of parabola}: \\ f(x)=x^2-(a+b)x+ab \\ \text{ Here, Leading coefficient is 1. So, direction of parabola will be upward.} \end{gathered}`
`\begin{gathered} Y-intercept: \\ \text{ Put }x=0\text{ and we will get }y=ab \end{gathered}`
`\begin{gathered} Zeros: \\ (x-a)(x-b)=0 \\ x=a,x=b \end{gathered}`

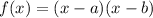
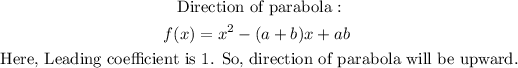
Answer:

The direction of parabola is upward, y intercept equals ab and zeros are x = a, b.