Question

What are the answers to all parts? All answers must be in 3 significant digits.

Answer 1

Part (a)

The initial momentum of the system can be expressed as,

`p_i=m_1u_1+m_2u_2`

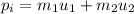
If the bullet is embedded in the block then the final moemntum of the system can be given as,

`p_f=(m_1+m_2)v`

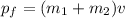
According to conservation of momentum,

`p_i=p_f`

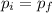
Plug in the known expressions,

`\begin{gathered} m_1u_1+m_2u_2=(m_1+m_2)v \\ v=(m_1u_1+m_2u_2)/(m_1+m_2) \end{gathered}`

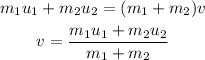
Substitute the known values,

`\begin{gathered} v=\frac{(19.6\text{ g)(318 m/s)+}(291\text{ g)(0 m/s)}}{19.6\text{ g+291 g}} \\ =\frac{6232.8\text{ gm/s}}{310.6\text{ g}} \\ \approx20.1\text{ m/s} \end{gathered}`

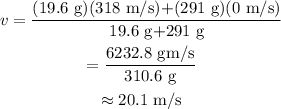
Thus, the final velocity of bullet after it is embedded in the block is 20.1 m/s.

Part (b)

The change in momentum of the system can be given as,

`\Delta p=p_f-p_i`

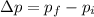
Substitute the known expressions,

`\Delta p=(m_1+m_2)v-(m_1u_1+m_2u_2)`

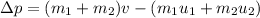
Substitute the known values,

`\begin{gathered} \Delta p=(19.6\text{ g+291 g)(20.1 m/s)-((19.6 g)(318 m/s)+(291 g)(0 m/s))} \\ =6243.06\text{ gm/s-}6232.8\text{ gm/s}-0\text{ g m/s} \\ =(10.26\text{ gm/s})(\frac{1\text{ kg}}{1000\text{ g}}) \\ \approx0.010\text{ kgm/s} \end{gathered}`

Thus, the change in the momentum of the system is 0.010 kgm/s.

Part (c)

The change in the momentum of the bullet can be expressed as,

`\Delta p=mu_{}-mv`

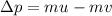
The final speed is in the opposite direction therefore, it will be taken as negative.

Plug in the known values,

`\begin{gathered} \Delta p=(19.6\text{ g)(318 m/s)-(}19.6\text{ g)(-299 m/s)} \\ =6232.8\text{ gm/s+}5860.4\text{ gm/s} \\ =(12093.2\text{ gm/s)(}\frac{1\text{ kg}}{1000\text{ g}}) \\ \approx12.1\text{ kgm/s} \end{gathered}`

Thus, the change in the momentum of the bullet is 12.1 kgm/s.