Question

Which statement explains why 13x - 13y = -26 shares a solution with this system of equations: 10x – 3y = 29 -3x + 10y = 55

Answer 1

Because -3x+10=55 is equal to 55,I can subtract -3x+10y from the left side of 10x-3y=29 and subtract 55 from its right side.

Subtracting equivalent expressions from each side of an equation do not change the solution to the equation.

Step-by-step explanation:

Given the system of equations

`\begin{gathered} 10x-3y=29 \\ -3x+10y=55 \end{gathered}`

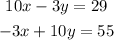
Subtracting -3x+10y from the left-hand side of 10x-3y=29 gives:

`\begin{gathered} 10x-3y-(-3x+10y)=29-55 \\ 10x-3y+3x-10y=-26 \\ 13x-13y=-26 \end{gathered}`

Therefore, we conclude that 13x-13y=-26 shares a solution with the system.

This is because -3x+10=55 is equal to 55, I can subtract -3x+10y from the left side of 10x-3y=29 and subtract 55 from its right side.

Subtracting equivalent expressions from each side of an equation does not change the solution to the equation.