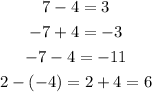Check below, please.
1) The sign rules are practical rules that tell us the sign in each operation.
2) So, let's enlist them providing an example of each:
Multiplication and Divison
"If the signs of each multiplier/dividend and multiplicand/divisor are the same then the product is positive.":
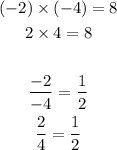
On the other hand, "If the signs of each multiplier/dividend and multiplicand/divisor are different then the product/quotient is negative."
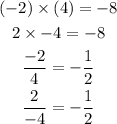
Addition:
"The magnitude of the addend indicates the sign". The greatest absolute value indicates the sign of the sum:
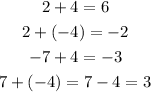
Subtraction
Similarly to addition, the greatest absolute value (or magnitude) is going to tell the sign of the subtraction: