This problem is a combination of functions, or doing a specific operation to two different function.
Here, we se the rule (fg)(5).
The product rule for functions can be written like this:
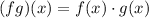
We will multiply our two functions, f(x) and g(x) together. Since we have an x value of 5, we can think of it like this:
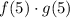
First, let's find f(5).
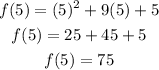
Next, let's evaluate g(5).
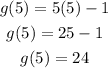
Finally, we will multiply f(5) and g(5).
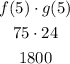
So, our final answer is 1800.