Question

A regular hexagon with a perimeter of 48 yd. Find the wares of the polygon and round to the nearest tenth.

Answer 1

166.3 square yards

Step-by-step explanation:

A regular hexagon has 6 equal sides.

Given that the perimeter = 48 yards

The side length, s:

`\begin{gathered} s=(48)/(6) \\ s=8\text{ yards} \end{gathered}`

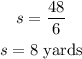
Next, we use the formula below for the area of a regular hexagon:

`A=\frac{3\sqrt[]{3}}{2}s^2`

Substitute 8 for s:

`\begin{gathered} A=\frac{3\sqrt[]{3}}{2}*8^2 \\ =96\sqrt[]{3} \\ \approx166.3\; yd^2\text{ (to the nearest tenth)} \end{gathered}`

The area of the regular hexagon is 166.3 square yards.

Method 2

A regular hexagon is divided into 6 equilateral triangles.

In this case:

The side length of the equilateral triangle = 8 yards

First, find the value of the height, h using the Pythagoras Theorem.

`\begin{gathered} 8^2=4^2+h^2 \\ h^2=8^2-4^2 \\ h^2=64-16 \\ h^2=48 \\ h=√(48) \\ h=6.93\text{ yds} \end{gathered}`

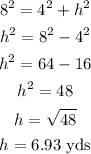
Next, find the area of one equilateral triangle:

`\begin{gathered} \text{Area}=(1)/(2)*\textcolor{red}{base}*\textcolor{green}{height} \\ =(1)/(2)*\textcolor{red}{8}*\textcolor{green}{6.93} \\ =27.72\; yd^2 \end{gathered}`

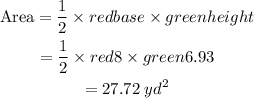
Since there are 6 equilateral triangles in the hexagon:

`\begin{gathered} \text{Area of the hexagon=6}* Area\text{ of one equilateral triangle} \\ =6*27.72 \\ =166.3\; yd^2 \end{gathered}`

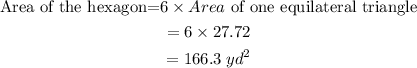
The area of the regular hexagon is 166.3 square yards.