Answer:
166.3 square yards
Step-by-step explanation:
A regular hexagon has 6 equal sides.
Given that the perimeter = 48 yards
The side length, s:
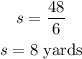
Next, we use the formula below for the area of a regular hexagon:
![A=\frac{3\sqrt[]{3}}{2}s^2](https://img.qammunity.org/2023/formulas/mathematics/college/p9jr4ioaqqbgapb4k9h1qtqi59sm9aoo5g.png)
Substitute 8 for s:
![\begin{gathered} A=\frac{3\sqrt[]{3}}{2}*8^2 \\ =96\sqrt[]{3} \\ \approx166.3\; yd^2\text{ (to the nearest tenth)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/lrfzwh6olfgnmak7pajzwbhuzfbz8si346.png)
The area of the regular hexagon is 166.3 square yards.
Method 2
A regular hexagon is divided into 6 equilateral triangles.
In this case:
The side length of the equilateral triangle = 8 yards
First, find the value of the height, h using the Pythagoras Theorem.

Next, find the area of one equilateral triangle:

Since there are 6 equilateral triangles in the hexagon:

The area of the regular hexagon is 166.3 square yards.