Question:
Solution:
Let the following equation:
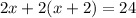
if we evaluate this equation at x=5, we obtain:
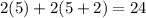
this is equivalent to:
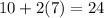
this is equivalent to:

that is:

so, if x = 5, then the equation holds. So that, we can conclude that the correct answer is:
The value of x from the set {1,3,5,7} that holds true for the equation is 7.
So, the width of the rectangle is 7 inches
and its length is 7 + 2 = 9 inches.