Question

How do I find the y intercept in a fraction

Answer 1

Both functions have the same slope

The linear equation does not have a y-intercept

The table and the grahp express an equivalent function

Explanation:

In order to compare, we must calculate the slope of the table, knowing that the equation in its slope and intercept form is the following:

`\begin{gathered} y=mx+b \\ \text{where m is the slope and b is y-intercept} \end{gathered}`

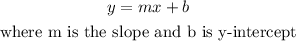
The formula to calculate the slope is the following:

`m=(y_2-y_1)/(x_2-x_1)`

The points are (-6, -9/2) and (4,3), replacing:

`m=(3-(-(9)/(2)))/(4-(-6))=(3+(9)/(2))/(4+6)=((15)/(2))/(10)=(15)/(20)=(3)/(4)`

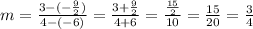
The slope is 3/4

Now, for b

x = 4

y = 3

m = 3/4

replacing:

`\begin{gathered} 3=(3)/(4)\cdot4+b \\ b=3-3 \\ b=0 \end{gathered}`

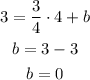
The equation is:

`y=(3)/(4)x`

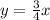
Therefore, the true statements are:

• Both functions have the same slope

,

• The linear equation does not have a y-intercept

,

• The table and the grahp express an equivalent function