To answer this question, we have:
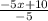
This is equivalent to the following:
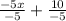
Then we have:
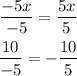
Therefore, we have:

If we simplify both fractions, we finally have:
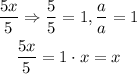
And
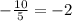
Then after simplification, we finally have:
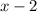
In summary, the process was as follows:
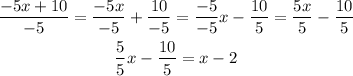
The final result is, then, x - 2.