To start with, we will first re-arrange the data set, in ascending order and then give the also show frequency
We can begin by finding the mode of the home prices
The mode is the home price with the highest frequency
From the table,
The mode
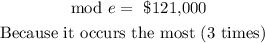
The median is the middle data of the data set there are 9 data set (An odd set)
![\begin{gathered} \operatorname{median}=((n+1)/(2))^(th) \\ \\ \text{where n=9} \end{gathered}]()
The median
![\begin{gathered} \operatorname{median}=(9+1)/(2)=5^{th\text{ }}data \\ \text{medain}=\text{ \$126,000} \end{gathered}]()
The mean is the average of the data set
It can be obtained by
![\begin{gathered} \bar{x}=\frac{\sum ^{}_{}fx}{\sum ^{}_{}f}=(70000+121000(3)+126000+135000(2)+180000+190000)/(9) \\ \\ \bar{x}=\operatorname{mean}=\text{ \$133222.222} \end{gathered}]()
The mean to the nearest thousand will be $133,000