The probability of getting a head on a fair coin toss is,
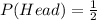
For a fair die, all its 8 faces have an equal probability of occurrence,
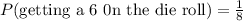
Note that both are independent events, so the probability of both occurring simultaneously will be equal to the product of the probabilities of them occurring individually.
So, the probability of getting a head on the coin toss and getting a 6 on the die roll, will be calculated as,
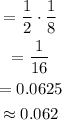
Thus, there is 0.062 probability of tossing a head and then rolling a number greater then 6.