Question

Determine the equation of the line that passes through the points (-2,3) and (4,15)

Answer 1

We are required to find the equation of a straight line passing through two given points .

First we can calculate the gradient / slope

`\begin{gathered} x_1=-2 \\ y_1=3 \\ x_2=4 \\ y_2=15 \end{gathered}`

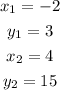
Calculating slope(m) below

`m=(y_2-y_1)/(x_2-x_1)`
`\begin{gathered} m=(15-3)/(4-(-2)) \\ m=(12)/(6) \\ m=2 \end{gathered}`

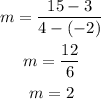
Using the formula y = mx + c at the point any of the two given points .... we can use ( 4 , 15 ) ... we have

`\begin{gathered} y=2x+c \\ x=4,y=15 \\ 15=2(4)+c \\ 15=8+c \\ c=7 \end{gathered}`

The required straight line equation will be obtained using y=mx+c as;

`y=2x+7`

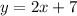
Here is a graph of the line

Hence the equation of the line is y=2x + 7