From the question given:
f(x) = 5x² + 40x - 3
comparing the above with ax² + bx + c
a = 5
b = 40
c=-3
The x - axis of the vertex can be gotten by simply finding the value of -b/2a
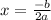
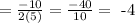
To get the y-axis of the vertex, simply substitute the value of x=-4 into the function given
That is ;
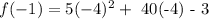
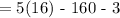
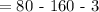
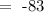
The function has a vertex at: (-4, -83)