We have a right triangle, and we can apply the trigonometric ratios here.
We have the following situation:
The question is about finding the values of 9 and 12. To do that, we can proceed as follows:
1. We know that the cosine, sine, and tangent ratios are given by:
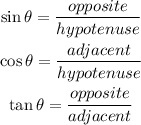
2. We have that the adjacent side to angle R is RS, and the opposite side to angle R is ST. Likewise, we have that the opposite side to angle T is RS and the adjacent side is ST.
3. We already know that:
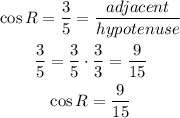
We know that trigonometric ratios are expressed in their reduced form. However, we can see here that we have to multiply by 3/3 the cosine ratio to find the original length of the side. Therefore, the side RS = 9 (units). We can find the other side using the Pythagorean Theorem:
![\begin{gathered} ST^2+RS^2=15^2 \\ ST^2+9^2=15^2 \\ ST^2=15^2-9^2 \\ \sqrt[]{ST^2}=\sqrt[]{15^2-9^2} \\ ST=\sqrt[]{225-81} \\ ST=\sqrt[]{144} \\ ST=12 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9zf86mgv6v6hhsbw2pret0y1kwk3ppqqx7.png)
4. Now, we got the necessary information to find the corresponding trigonometric ratios:

Therefore, we have:
A. Cos T = 12/15 (It is an option).
B. sinT = 3/5 (It is NOT an option sinT = 4/5).
C. sinR = 4/5 (It is an option).
D. cosR = 9/15 (It is NOT an option cosR = 12/15).
In summary, the answer choices that are possible trigonometric ratios for the triangle above are:
A. Cos T = 12/15
C. sinR = 4/5 (It is an option).