Question

(4,3) and (6,5) are end points of the diameter of a circle. Find the center and radius.

Answer 1

We know two points that are the endpoints of a diameter of a circle.

We can picture them as:

The center will be the midpoint of that segment and the diameter will be the length of that segment, equal to the distance between the endpoints.

We can start calculating the center.

As the center is the midpoint between the endpoints, the x-coordinate will be the average of the x-coordinates of the endpoints. The same can be said for the y-coordinate.

Then, we can find the coordinates of the center as:

`\begin{gathered} x_C=(x_A+x_B)/(2)=(4+6)/(2)=(10)/(2)=5 \\ \\ y_C=(y_A+y_B)/(2)=(3+5)/(2)=(8)/(2)=4 \end{gathered}`

The coordinates for the center are (5, 4).

Now, we can calculate the diameter as the distance between the endpoints:

`\begin{gathered} d=√((x_A-x_B)^2+(y_A-y_B)^2) \\ d=√((4-6)^2+(5-3)^2) \\ d=√((-2)^2+(2)^2) \\ d=√(4+4) \\ d=√(8) \\ d=2√(2) \end{gathered}`

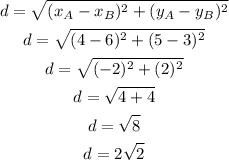
The diameter is 2√2 or approximately 2.828.

We can express the radius as half the diameter:

`r=(D)/(2)=(2√(2))/(2)=√(2)\approx1.414`

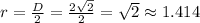
Answer:

Center: (5, 4)

Radius: √2 (or approximately 1.414).