For the quadratic equation -4x^2 - 7x + 3 = 0, the value oc coefficients are,
a = -4, b = -7 and c = 3.
Determine the value of determinant for the quadratic equation.
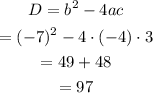
The value of determinant is greater than 0, so quadratic equation has two different real roots.
Determine the roots of the equation by using quadratic formula.
![\begin{gathered} x=\frac{-(-7)\pm\sqrt[]{(-7)^2-4\cdot(-4)\cdot3}}{2\cdot(-4)} \\ =\frac{7\pm\sqrt[]{49+48}}{-8} \\ =\frac{7\pm\sqrt[]{97}}{-8} \\ =-(7)/(8)\pm\frac{\sqrt[]{97}}{-8} \\ =-(7)/(8)+\frac{\sqrt[]{97}}{8},-(7)/(8)-\frac{\sqrt[]{97}}{8} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/hs6msva0bptk2x6gzyv9hbw8py0swn6zes.png)
So root of the equation are,
![-(7)/(8)+\frac{\sqrt[]{97}}{8}\text{ and -}(7)/(8)-\frac{\sqrt[]{97}}{8}](https://img.qammunity.org/2023/formulas/mathematics/college/mh3zjh64thuwmgaga1fubhdmfjvgcvxwis.png)