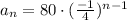Answer:
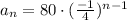
Step-by-step explanation:
We can see that 20 is equal to 80 divided by 4 and 5 is equal to 20 divided by 4. Additionally, the sign change for every term. So, the explicit formula for an is:
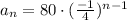
So, we can prove that this equation applies for the first 3 terms as:
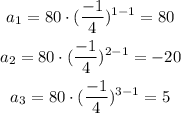
Therefore, the answer is: