Question

The explicit rule for a sequence isan=9-14nwhat is the recursive rule for the sequence?A) an=an-1-9a1=5B) an=an-1-9a1=14C) an=an-1-14a1=-5D) an=an-1-14a1=9

Answer 1

The Solution:

Given the explicit rule of a sequence below:

`a_n=9-14n`

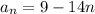
We are required to determine the recursive rule for the sequence.

Step 1:

Find the first term, that is, when n=1.

`\begin{gathered} a_1=9-14(1)=9-14=-5 \\ \\ a_1=-5 \end{gathered}`

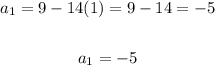
Step 2:

Find the second to the last term, that is, when n=n-1.

`a_(n-1)=9-14(n-1)=9-14n+14=9+14-14n=23-14n`

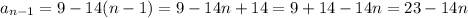
Step 3:

Find the d, the common difference.

`\begin{gathered} d=a_n-a_(n-1)=9-14n-(23-14n)=9-14n-23+14n \\ \\ d=9-23-14n+14n=-14 \\ \\ d=-14 \end{gathered}`

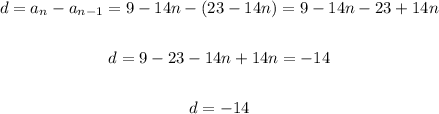
Recall:

The recursive rule for a linear sequence is:

`a_n=a_(n-1)+d`

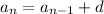
Substituting -14 for d, we get

`a_n=a_(n-1)-14`

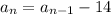
Thus, the recursive rule for the sequence is:

`\begin{gathered} a_(n)=a_(n-1)-14 \\ \\ a_1=-5 \end{gathered}`

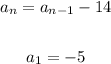
Therefore, the correct answer is [option 3]