Question

7x-60+x^2 factor each polynomial completely. If a polynomial is prime, state this.

Answer 1

(x-5)(x+12).

Step-by-step explanation:

Given the polynomial:

`7x-60+x^2`

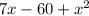
First, we write it in the standard form of a polynomial:

`x^2+7x-60`

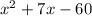
Next, multiply the first and last term:

`x^2*-60=-60x^2`

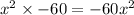
Pick factors of the product that add up to the middle term:

`\begin{gathered} -60x^2=12x\text{ and -5x} \\ 12x-5x=7x \end{gathered}`

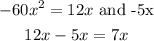
Therefore:

`\begin{gathered} x^2+7x-60=x^2+12x-5x-60 \\ =x(x+12)-5(x+12) \\ =(x-5)(x+12) \end{gathered}`

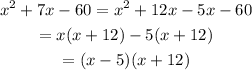
The factored form of the polynomial is (x-5)(x+12).

Note: A polynomial is prime if it cannot be factored. Since the example above can be factored, it is not prime.