Answer: the mass of O2 present in the sample under the given conditions is 0.1495g
Step-by-step explanation:
The question requires us to calculate the mass of oxygen gas (O2) that is present under the given conditions:
Volume = 120.0 mL
Pressure = 700.0 mmHg
Temperature = 15°C
To solve this problem, we can apply the equation of ideal gases, which states:
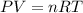
where P refers to the pressure of the system, V is the volume of gas, R is the constant of gases (R = 0.0821 L.atm/K.mol) and T is the temperature of the gas. Note that, according to the units used for the constant of gases, we need to use pressure in units of atm, V in units of liter, n is given in moles and T must be used in Kelvin.
We can rearrange the equation above to calculate the number of moles of the gas:
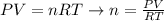
And, knowing that the number of moles of a susbtance corresponds to the ratio between the mass of the sample (m) and the molar mass of the compound (M), we can write:
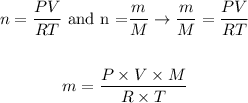
Before applying the equation above, we need to convert the given values of pressure, volume and temperature to the appropriate units:
- Pressure:
1 atm corresponds to 760 mmHg, thus:
760 mmHg ----------- 1 atm
700.0 mmHg ------- x
Solving for x, we have that 700.0 mmHg corresponds to 0.9211 atm.
- Volume:
1 L corresponds to 100 mL, thus:
1000 mL ----------- 1 L
120.0 mL ---------- y
Solving for y, we have that 120.0 mL corresponds to 0.1200 L.
- Temperature:
0°C corresponds to 273.15 K, thus we can add 273.15 to the given temperature value to obtain the corresponding temperature:
T(K) = 15 + 273.15 = 288.15 K
Therefore, 15°C corresponds to 288.15 K.
Now that we have all values in the correct unit (P = 0.9211 atm, V = 0.1200 L and T = 288.15 K), we can apply these values to our rearranged equation to obtain the mass of O2. The molar mass of O2 is 31.998 g/mol, thus we have:

Therefore, the mass of O2 present in the sample under the given conditions is 0.1495g.