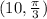Answer:
Step-by-step explanation:
Given the rectangular coordinates of a point as;
![\begin{gathered} (-5,-5\sqrt[]{3}) \\ \text{where }x=-5,y=-5\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/kxv01dfoxm1i4yev7133y237g17q0a4g7m.png)
A polar coordinate is generally given in the form;
![\begin{gathered} (r,\theta) \\ \text{where }r=\sqrt[]{x^2+y^2} \\ \theta=\tan ^(-1)((y)/(x)) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/n3m290uzfbx2ftq65bfgree88noqvm11nk.png)
Let's go ahead and substitute the given values into the equation for determining r and evaluate;
![\begin{gathered} r=\sqrt[]{(-5)^2+(-5\sqrt[]{3})^2} \\ r=\sqrt[]{25+25(3)} \\ r=\sqrt[]{25+75} \\ r=\sqrt[]{100} \\ r=10 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4roralqarxj0rxc6dad86lavqtku8heyiq.png)
Let's also substitute the given values into the equation for determining theta and evaluate;
![\begin{gathered} \theta=\tan ^(-1)(\frac{-5\sqrt[]{3}}{-5}) \\ \theta=\tan ^(-1)(\sqrt[]{3}) \\ \theta=(\pi)/(3) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/q0vqc15o83lidb9fd371r096y6ui8za2t8.png)
Therefore, the polar coordinates of the given point are;