Question

The function y = (x2 + 1)(x2 + 2) has how many x-intercepts? options:a) 0 b) 1 c) 2 d) 3

Answer 1

Step-by-step explanation

We must find the number of x-intercepts present in the function:

`y=(x^2+1)(x^2+2)`

The x-intercepts are the points where the graph of the function intercepts the x-axis which implies that y=0 at those points. Then the number of x-intercepts is equal to the number of solutions of the equation y=0:

`0=(x^2+1)(x^2+2)`

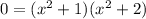
We have that the product of two expressions is equal to 0. This means that the solutions to this equation are also the solutions to the two equations given by equalizing each term to 0:

`\begin{gathered} x^2+1=0 \\ x^2+2=0 \end{gathered}`

We can substract 1 from both sides of the first equation and 2 from both sides of the second equation:

`\begin{gathered} x^2+1-1=0-1\rightarrow x^2=-1 \\ x^2+2-2=0-2\rightarrow x^2=-2 \end{gathered}`

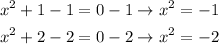
As you can see in both equation the square of x is a negative number. This is false for any real value of x which means that the original equation has no real solutions. Therefore the value of y is never 0 and the function has no x-intercepts.

Answer

Then the answer is option a).