we have the polar equation
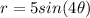
using a graphing tool
The arc length is given by the formula
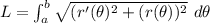
where
Find out r' (a derivative of r)
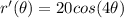
a=0
b=pi/4
substitute given values in the formula
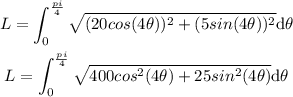
Solve the integral
The answer is
one minute, please
The arc length is L=10.723 units (three decimal places)