We are given the equation of a parabola. Let's remember the general form for this equation:

The given equation is:
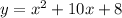
Therefore, the coefficients are:
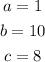
Now we will rewrite the equation to the form:
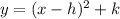
First we will change the equation in the following way:
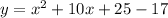
Now we can factor:
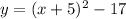
since the term (x+5)^2 is multiplied by a positive constant, this means that the parabola opens up.
The vertex of the parabola is the point (h,k), in this case, we have:

The axis of symmetry for a parabola is x = h, therefore, the axis of symmetry for this parabola is:

The y-intercept is the point where x = 0, therefore, making x zero in the equation we get:
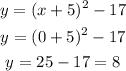
Therefore the y-intercept is y = 8.