Question

Historically, “...Factorization was first considered by ancient Greek mathematicians in the case of integers.In mathematics, factorization or factoring consists of writing a number or another math object as a product of several factors, usually smaller or simpler objects of the same kind. For example, 3 × 5 is a factorization ofthe integer 15, and the factorization of the polynomial x2 – 4 is (x – 2)(x + 2)”. A student once asked,“When Will I Ever Use This In Real Life? Let’s explore a real world possibility task below. A teacher assigned the following task below for students to work in groups and apply their factoring skills he taught them in class. TASK: Factoring and the length vs width dilemma!!: The groundskeeper at the local community Zoo would like to build a new enclosure around the large reptile house located in the North West Corner of the Zoo. The area of the shape represented algebraically is 42k2 – 30k ft2; however, he needs help to figure out the blueprint measurements for the perimeter of the enclosure algebraically. Shown below is a map of the Zoo.Group D completed the task and made the following claims below.1) The shape of the large reptile house is a rectangle2) They used prime factorization and the sum of common factors to identify the GCF as 5k 3) The factored form of 42k2 – 30k ft is (5k ft)(7k – 5 ft)4) The length can be represented by (7k – 5ft) and the width can be represented by (5k ft)5) The perimeter of the reptile house algebraically can be represented by 24k – 10 feet6) They concluded that their blueprint response made sense and wanted to share their results with the zookeeperCreate a written response that express and demonstrates your point of view about Group Ds’ work and include the following in your written response. (Hint: R.A.C.E) Write a claim. Statements written in sentences that expresses your point of view about the claim(s) made in the scenario given above. Provide evidence/justification and supported reasoning using any method of your choice Write a counterclaim. Write a sentence that contradicts the claim made and clearly states your position. Explain the counterclaim you are making. The more “real” you make the opposing position, the more “right” you will seem when you disprove it using clear sentences and mathematical language. State a clear conclusion. A concluding statement that summarizes your point of view/claim

Answer 1

Given:

statement 1) The shape of the large reptile house is a rectangle.

Yes the statement is true because it is observed that from the blue print of zoo. the reptile house is in the ractangular shape ( as opposite side are parallel and each interior angle is of 90 degree)

Statement 2) They used prime factorization and the sum of common factors to identify the GCF as 5k

Claim: the statement 2) is incorrect

The area is,

`A=42k^2-30k`

The GCF is given by,

`\begin{gathered} 42k^2-30k \\ 42=2*3*7 \\ 30=2*3*5 \\ 3\text{ is the greatest fctaors appears on both prime factorization} \\ \text{thuse, GCF is 3k} \end{gathered}`

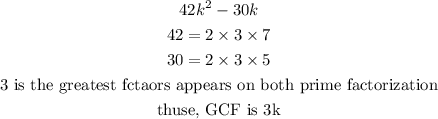
Hence, the statement 2) is incorrect

Statement 3) is incorrect because,

`\begin{gathered} 42k^2-30k=6k(7k-5) \\ \text{the factors are 6k ft and (7k-5) ft} \end{gathered}`

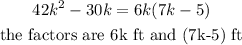
Statement 4) The length can be represented by (7k – 5ft) and the width can be represented by (5k ft)

Area of rectangle is given by,

`\begin{gathered} A=L* W \\ A=42k^2-30k \\ A=(7k-5)6k \\ L=(7k-5)\text{ and W=6k} \end{gathered}`

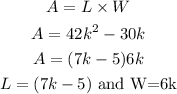
The statement 4) is incorrect.

Statement 5) The perimeter of the reptile house algebraically can be represented by 24k – 10 feet



The perimeter is given by,

`\begin{gathered} P=2W+2L \\ P=2(6k)+2(7k-5) \\ P=12k+14k-10 \\ P=26k-10 \end{gathered}`

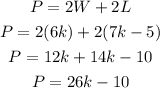
Hence, the statement 5) is incorrect .

6) Conclusion:

The blueprint changes should be

The GCF=3k

the fractors are (6k) (7k-5)

Length=7k-5 and width=6k

Perimeter=26k-10

After these changes they can share their results with the zookeeper.