Question

Consider the line = -3x-9y= -4What is the slope of a line perpendicular to this line?What is the slope of a line parallel to this line?

Answer 1

If two lines with slopes m₁ and m₂ are perpendicular, then:

`m_1* m_2=-1`

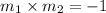
Isolate y to write the given line in slope-intercept form. Identify the slope of the line as the coefficient of x and find the slope of a line perpendicular to it using the given relationship between the slopes of perpendicular lines.

Starting from the equation:

`-3x-9y=-4`

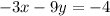
Isolate y:

`\begin{gathered} \Rightarrow3x+9y=4 \\ \Rightarrow9y=4-3x \\ \Rightarrow y=(4)/(9)-(3)/(9)x \\ \\ \therefore y=-(1)/(3)x+(4)/(9) \end{gathered}`

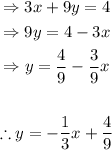
Then, the slope of the given line is -1/3. Let m be the slope of a line perpendicular to -3x-9y=-4. Then:

`\begin{gathered} (-(1)/(3))* m=-1 \\ \Rightarrow m=(-1)/((-(1)/(3)))=3 \\ \\ \therefore m=3 \end{gathered}`

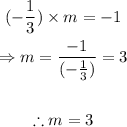
Therefore, the slope of a line perpendicular to the given line is 3.

Two parallel lines have the same slope.

Therefore, the slope of a line parallel to the given line is -1/3.