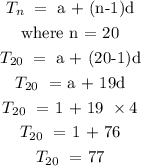Question

write a variable expression to describe the rule of each progression then calculate the term 20 or 20 term1.) 6,12,18,24,...2.)3,6,9,12,...3.)1,5,9,13...

Answer 1

1) 6, 12,18,24

The rule used here is: Arithmetic Progression or Linear sequence

From the data above:

a = 6, d = 6

`\begin{gathered} T_{n\text{ }}=\text{ a + (n-1)d} \\ \text{where n = 20} \\ T_{20\text{ }}=\text{ a + (20-1)d} \\ T_{20\text{ }}\text{ = a + 19d} \\ T_{20\text{ }}\text{ = 6 + 19}*6 \\ T_{20\text{ }}\text{ = 6 + 114} \\ T_{20\text{ }}\text{ = 120} \end{gathered}`

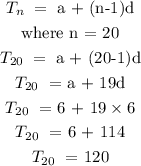
2) 3,6,9,12

The rule used here is: Arithmetic Progression or Linear sequence

From the data above:

a = 3, d = 3

`\begin{gathered} T_{n\text{ }}=\text{ a + (n-1)d} \\ \text{where n = 20} \\ T_{20\text{ }}=\text{ a + (20-1)d} \\ T_{20\text{ }}\text{ = a + 19d} \\ T_{20\text{ }}\text{ = 3 + 19 }*3 \\ T_{20\text{ }}\text{ = 3 + 57} \\ T_{20\text{ }}\text{ = 60} \end{gathered}`

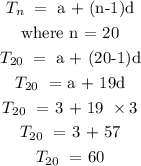
3) 1,5,9,13

The rule used here is: Arithmetic Progression or Linear sequence

From the data above:

a = 1, d = 4

`\begin{gathered} T_{n\text{ }}=\text{ a + (n-1)d} \\ \text{where n = 20} \\ T_{20\text{ }}=\text{ a + (20-1)d} \\ T_{20\text{ }}\text{ = a + 19d} \\ T_{20\text{ }}\text{ = 1 + 19 }*4 \\ T_{20\text{ }}\text{ = }1\text{ + 76} \\ T_{20\text{ }}\text{ = }77 \end{gathered}`