To solve the given equation, we need to perform any needed calculation to isolate X on it.
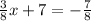
The first step is to multiply both sides by 8, as follows:
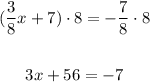
Now we subtract 56 to both sides:
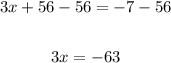
Now we divide both sides by 3:

From the solution we developed above, we are able to conclude that the answer of the given equation is:
