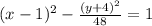Question

I need help on this :)vertices at (0, -4) and (2, -4)

Answer 1

EXPLANATION :

From the problem, we have a hyperbola with foci at (-6, -4) and (8, -4) and vertices at (0, -4) and (2, -4)

Plot these points to the rectangular coordinate system :

From here, we can say that the hyperbola is horizontal and the graph of it will look like this.

We need to find the center (h, k) of the hyperbola which is the midpoint of the vertices

The midpoint will be :

`((0+2)/(2),(-4+(-4))/(2))\rightarrow(1,-4)`

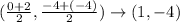
So the center is at (h, k) = (1, -4)

The standard form of the equation of the hyperbola is :

`((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1`

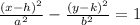
where a = distance between the center and one of the vertices

Solve for the value of a.

`\begin{gathered} \text{ The distance between the center \lparen1, -4\rparen and \lparen2, -4\rparen is 1 unit.} \\ \text{ Then :} \\ a=1 \end{gathered}`

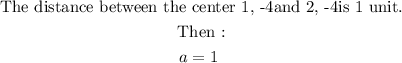
The distance between the center and one of the foci is denoted as c.

Solve for c :

`\begin{gathered} \text{ The distance between the center \lparen1, -4\rparen and \lparen8, -4\rparen is 7 units.} \\ \text{ Then :} \\ c=7 \end{gathered}`

Note that :

`c^2=a^2+b^2`

We already have the value of a = 1 and c = 7, and we need the value of b to complete the equation of the hyperbola :

`\begin{gathered} c^2=a^2+b^2 \\ 7^2=1^2+b^2 \\ 49=1+b^2 \\ b^2=48 \end{gathered}`

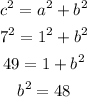
Plug in a = 1 and b^2 = 48 to the equation of the hyperbola with center of (h, k) = (1, -4)

`\begin{gathered} ((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1 \\ \\ ((x-1)^2)/(1^2)-((y+4)^2)/(48)=1 \\ \\ (x-1)^2-((y+4)^2)/(48)=1 \end{gathered}`

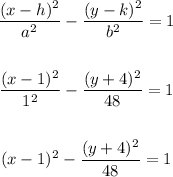
ANSWER :

The equation of the hyperbola is :

`(x-1)^2-((y+4)^2)/(48)=1`