Question

Rewrite y = a(4)¹/6 in the form y = a(1+r) or y = a(1-r). Then state the growth or decay rate.The rate is%.This is arate.

Answer 1

y = a[1 + 0.26]^t

Rate = 0.26

This is a growth rate

Step-by-step explanation:

If we have the following equation modelling a growth or decay.

`y=a[1+r]^t`

then if r < 0, then the above equation models decay. If a > 0, then the above equation models growth.

We can rewrite our equation y = a(4)¹/6 as

`a(4^(1/6))^t`

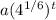
Now

`4^(1/6)=(2^2)^(1/6)=2^(2/6)=2^(1/3)=\sqrt[3]{2}\approx1.26`

Therefore,

`y=a(\sqrt[6]{4})^t\approx a[1.26]^t`

which can also be written as

`\boxed{y=a\left[1+0.26\right]^t.}`

which is our answer!

As can be seen from the above equation, the rate is r = 0.26.

Now r = 0.26 > 0, which means that the equation above models a growth.

Hence, to summerise

y = a[1 + 0.26]^t

Rate = 0.26

This is a growth rate