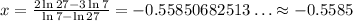Question

-Exponential and Logarithmic Functions-Solve the following. Round the answer to the nearest ten thousandth.

Answer 1

We want to find the solutions for the following equation

`7^(x+3)=27^(x+2)`

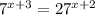
Using the following property

`\ln a^b=b\ln a`

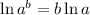
we can apply the natural log on both sides of our equation and rewrite it

`\begin{gathered} 7^(x+3)=27^(x+2) \\ \ln 7^(x+3)=\ln 27^(x+2) \\ (x+3)\ln 7=(x+2)\ln 27 \end{gathered}`

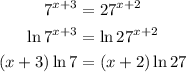
Using the distributive property, we have

`\begin{gathered} (x+3)\ln 7=(x+2)\ln 27 \\ x\ln 7+3\ln 7=x\ln 27+2\ln 27 \end{gathered}`

Rewritting the expression isolating the unknown value, we have

`\begin{gathered} x\ln 7+3\ln 7=x\ln 27+2\ln 27 \\ x\ln 7-x\ln 27=2\ln 27-3\ln 7 \\ x(\ln 7-\ln 27)=2\ln 27-3\ln 7 \\ x=(2\ln27-3\ln7)/(\ln7-\ln27) \end{gathered}`

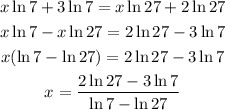
Now, using a calculator we can find our result.

`x=(2\ln27-3\ln7)/(\ln7-\ln27)=-0.55850682513\ldots\approx-0.5585`