We are given the following radical expression.
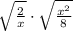
Let us simplify the above expression.
Recall the product rule of radicals given by
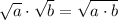
Apply the above rule to the given expression.
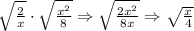
Recall the quotient rule of radicals given by
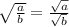
Apply the above rule to the given expression.
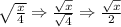
Therefore, the simplified expression is
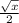
Option A is the correct answer.