From the statement we know that:
• the total distance travelled is 2d, being d the distance to the comic store,
,
• the forward velocity is v1 = 45 ml/h,
,
• the backward velocity is v2 = 35 ml/h,
,
• the total time spent on the travel is t = 4 h.
Now, we can write the total distance travelled in the following way:
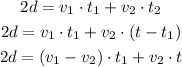
Where:
• t1 is the time for the travel to the comic book store,
,
• t2 is the time for the return from the comic book store.
Now, we also know that the distance is equal to the product between the time and the velocity, so:
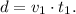
Replacing the last equation in the equation above, we have:
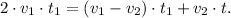
Now, we solve the last equation for v1:
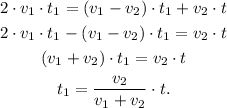
Replacing the values of the velocities v1 and v2, and the time t we get:
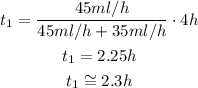
Answer
Rounded to one decimal place, it takes 2.3 hours to get to the comic book store.