Ms. Watson spent $11.90 to buy a total of 20 candy bars and lollipops. A candy bar cost $1.40 and a lollipop costs $0.25. How many candy bars did Ms. Watson buy?

Question

asked May 19, 2023 857 views

1 Answer

BassMHL · Answer 1 · 2023-05-22T16:08:36+0000

Let:

x = Number of candy bars

y = Number of lollipops

a = cost of a candy bar

b = cost of a lollipop

Ms. Watson spent $11.90 to buy a total of 20 candy bars, so:

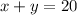
and:

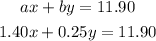
$\begin{gathered} ax+by=11.90 \\ 1.40x+0.25y=11.90 \end{gathered}$

Let:

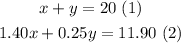
$\begin{gathered} x+y=20_{\text{ }}(1) \\ 1.40x+0.25y=11.90_{\text{ }}(2) \end{gathered}$

From (1) solve for y:

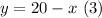
$y=20-x_{\text{ }}(3)$

Replace (3) into (2):

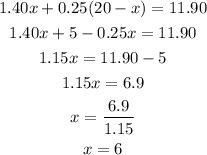
$\begin{gathered} 1.40x+0.25(20-x)=11.90 \\ 1.40x+5-0.25x=11.90 \\ 1.15x=11.90-5 \\ 1.15x=6.9 \\ x=(6.9)/(1.15) \\ x=6 \end{gathered}$

Replace the value of x into (3):

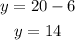
$\begin{gathered} y=20-6 \\ y=14 \end{gathered}$

Ms watson bought 6 candy bars and 14 lollipops