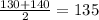Basically the idea is to determine which measurements change when you change one element. Supose that the number of pages he thought the longest book had is represented by h
For instance, the average will change, since the new avarage will be
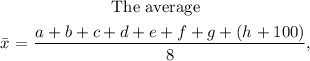
This is also the case for the standard deviation, you can check the formula and see that it changes. However, the median and the interquartile range will not change.
For example, consider that the number of pages of the book at the beggining was
![a<p>then the median is (d+e)/2, no matter what the value of h is, that is, the highest. Also, a,b is the first quartil, c,d the second, e,f, the third and g,h the fourth no matter the value of h (it can be change by h+100).</p><p></p><p>Let's make a concrete example. Suppose that the number of pages was </p>[tex]100,110,120,130,140,150,160,170]()
Then the mean is
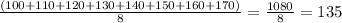
And the median is
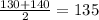
But after he figured out that he have miscounted the number of pages of the last book, we have that the correct numbers of pages is
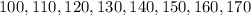
and the correct mean is
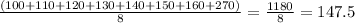
so he had to recalculate the mean. On the other hand, the median is still the same, since the values of the middle, that is, 130 and 140 have not changed. Then, the median is