Question

Solve the right triangle, ΔABC, for the missing side and angles to the nearest tenth given sides a = 13.2 and b = 17.7.A. A = 48.2 , B = 41.8 , c = 22.1B. A = 41.8 , B = 48.2 , c = 11.8C. A = 36.7 , B = 53.3 , c = 22.1D. A = 36.7 , B = 53.3 , c = 11.8

Answer 1

We have to solve the right triangle.

We know two of the sides: a = 13.2 and b = 17.7.

This are the two legs, and we have to find c, the hypotenuse and A and B, the two non-right angles.

We can calculate c as:

`\begin{gathered} c^2=a^2+b^2 \\ c^2=13.2^2+17.7^2 \\ c^2=174.24+313.29 \\ c^2=487.53 \\ c=√(487.53) \\ c\approx22.1 \end{gathered}`

We can now find the angles using trigonometric ratios.

We can find A as:

`\begin{gathered} \tan A=(Opposite)/(Adjacent)=(a)/(b)=(13.2)/(17.7)\approx0.7458 \\ \\ A\approx\arctan(0.7458)\approx36.7\degree \end{gathered}`

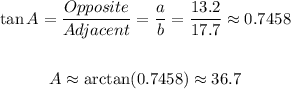
We can find B as:

`\begin{gathered} \tan B=(b)/(a)=(17.7)/(13.2)\approx1.3409 \\ \\ B\approx\arctan(1.3409)\approx53.3\degree \end{gathered}`

Answer:

A = 36.7°, B = 53.3°, c = 22.1 [Option C]