Question

Determine whether the triangles are similar and justify your answer

Answer 1

a)

Answer:

Since the ratio of their corresponding sides are equal the two triangles are similar.

`\begin{gathered} (AB)/(BC)=(15)/(36)=(5)/(12) \\ (XZ)/(YZ)=(10)/(24)=(5)/(12) \\ (AB)/(BC)=(XZ)/(YZ)=(5)/(12) \end{gathered}`

Step-by-step explanation:

Given the triangles in the attached image;

We want to confirm if they are similar.

For them to be similar the ratio of their corresponding sides must be equal.

`(AB)/(BC)=(XZ)/(YZ)=\text{ constant}`

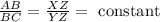
Given;

`\begin{gathered} AB=15 \\ BC=36 \\ XZ=10 \\ YZ=24 \end{gathered}`

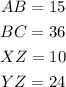
Substituting to get the ratio of the sides;

`\begin{gathered} (AB)/(BC)=(15)/(36)=(5)/(12) \\ (XZ)/(YZ)=(10)/(24)=(5)/(12) \\ (AB)/(BC)=(XZ)/(YZ)=(5)/(12) \end{gathered}`

Since the ratio of their corresponding sides are equal the two triangles are similar.