Question

A 15 fladder leans against the side of a house. The bottom of the ladder is 7 A away from the side of the house. Find x,the angle of elevation of the ladder. Round your answer to the nearest tenth of a degree.

Answer 1

We are asked to find the angle x as shown in the given figure.

Recall the trigonometric ratio,

`\cos \theta=\frac{\text{adjacent}}{\text{hypotenuse}}`

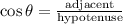
With respect to angle x, the adjacent side is 7 ft and the hypotenuse is 15 ft.

Let us substitute these values into the above formula

`\cos x=(7)/(15)`

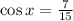
Take the inverse of cos function

`\begin{gathered} x=\cos ^(-1)((7)/(15)) \\ x=62.2\degree \end{gathered}`

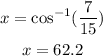
Therefore, the angle of elevation of the ladder is 62.2