Question

The length of a rectangle is 1 inches more than the width. The area is 30 square inches. Find the dimensions

Answer 1

Let's call the length of this rectangle as x and the width as y.

"The length of a rectangle is 1 inches more than the width. "

This means that our x value is 1 unit bigger than the y value. Writing this as an equation

`y+1=x`

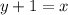
"The area is 30 square inches. "

The area of a rectangle is given by the product of its sides. Then, we have the following equation

`xy=30`

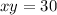
Using our x value from the first equation, we have

`\begin{gathered} xy=30 \\ (y+1)y=30 \\ y^2+y-30=0 \end{gathered}`

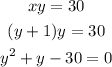
We have a second degree equation, we find the roots by using Bhaskara's formula.

The roots of this equation are

`\begin{gathered} y_(\pm)=\frac{-1\pm\sqrt[]{1^2-4\cdot1\cdot(-30)}}{2\cdot1}=(-1\pm11)/(2) \\ \Rightarrow\begin{cases}y_-=-6 \\ y_+=5\end{cases} \end{gathered}`

Since we're dealing with a measurement, the negative root doesn't make any sense, therefore, our width is 5 inches. Now that we have the width, we can substitute in any of the equations this value to find the length

`y+1=x\Rightarrow5+1=x\Rightarrow x=6`

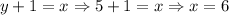
The length of our rectangle is 6 inches.