Question

An AC generator creates sinusoidal emf in a circuit with the total resistance of 220. Ω.. The peak value of the current is 1.72 A.a) Determine rms current.b) Determine rms voltage across the resistance.c) Calculate the average power dissipated in the circuit.d) Assuming the frequency f of the AC current being 60 Hz, write down the expression of the ACcurrent as the function of time.

Answer 1

Given data

*The given total resistance R = 220.0 Ω

*The given peak value of the current is I_max = 1.72 A

*The given frequency is f = 60 Hz

(a)

The formula for the rms current is given as

`I_(rms)=\frac{I_(\max )}{\sqrt[]{2}}`

Substitute the known values in the above expression as

`\begin{gathered} I_(rms)=\frac{1.72}{\sqrt[]{2}} \\ =1.21\text{ A} \end{gathered}`

(b)

The rms voltage across the resistance is calculated as

`\begin{gathered} V_(rms)=I_(rms)* R \\ =(1.21)(220.0) \\ =266.2\text{ V} \end{gathered}`

(c)

The average power dissipated in the circuit is calculated as

`\begin{gathered} P_(avg)=V_(rms)I_(rms)_{}_{} \\ =(266.2)(1.21) \\ =322.10\text{ W} \end{gathered}`

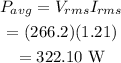
(d)

The expression for the AC current as the function of time is given as

`\begin{gathered} I(t)=I_(\max )\sin (2\pi ft) \\ =1.72\sin (2*3.14*60.0* t) \\ =1.72\sin (376.8t) \end{gathered}`