Question

There’s t h r e e different functions that I have to match with the ones that are on the box

Answer 1

Since function A has 2 zeros, A has the form:

`A(x)=f(x)(x-2)(x-4)`

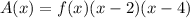
Then, if we divide it by (x-2), we get:

`(A(x))/((x-2))=f(x)(x-4)`

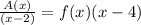
And the remainder is zero.

Additionally, we know that A has 2 unique zeros: then, it cannot have a repeated factor of (x-4).

If we plot function A, we get:

The graph seems to be a polynomial of grade 3, and the leading term is negative.

Notice that

`\lim _(x\to\infty)A(x)=-\infty`

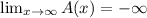
According to the graph we got. On the other hand:

`\lim _(x\to-\infty)A(x)=\infty`

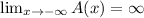
Then. Function A matches:

1. When I am divided by (x-2) the remainder is 0.

2. f(4)=0

3. One of my end behaviors is: As x->-infinite, f(x)->infinite

As for function B.

The graph indicates that there are 3 unique zeros: x=1,2,4. That it represents a polynomial of grade 4 and the leading term is positive since the function grows when x->infinite and x->-infinite.

Thus, function B matches:

1. When I am divided by (x-2) the remainder is 0.

2. I have a positive leading coefficient.

3. f(4)=0

4. I have 3 roots

5. One of my end behaviors is: As x->infinite, f(x)->infinite

6. (x-1) is one of my factors

7. I am a Quartic

8. One of my end behaviors is: As x->-infinite, f(x)->infinite

Finally, regarding function C.

`C(x)=x^3+4x^2-3x-18=(x-2)(x+3)^2`

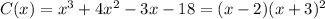
Then, C(x) is a polynomial of grade 3, and its limits are:

`\lim _(x\to\infty)C(x)=\infty,\lim _(x\to-\infty)C(x)=-\infty`

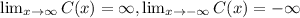
Then, the answers for function C are:

1. When I am divided by (x-2) the remainder is 0.

2. I have a positive leading coefficient. (leading coefficient is 1)

3. I have 3 roots

4. One of my end behaviors is: As x->infinite, f(x)->infinite