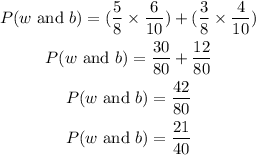Solution:
Let white balls be w, and black balls be b;
In the first bag;
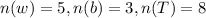
But, in the second bag;
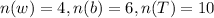
(i) The probability that both balls drawn from each bag are white is;
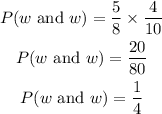
(ii) The probability that both balls drawn from each bag are black is;
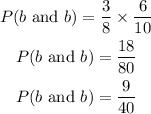
(iii) The probability that one is white and another is black is;