Part a) If in 1970 the 83% of 30-year-olds earned more than their parents, then if we choose at random one 30-year-old person the probability that he/she earned more than his/her parents when they were 30 years old is 0.8300.
Part b) The probability of two randomly selected 30-year-olds in 1970 earned more than their parents at age 30 is 0.83*0.83= 0.6889.
Part c) For this part we use binomial probability. The probability of interest is equal to the probability that at least 9 earned more than their parents. The probability that at least 9 earned more than their parents is:
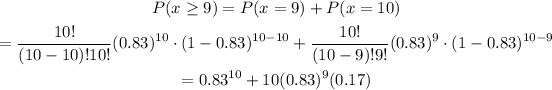
computing we get 0.4730.
Part d) Solving similarly as part c) but considering that the probability for the year 2014 instead of the one for 1970 we get:
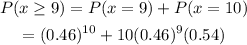
computing we get 0.0054.