Question

Which function is used to find y, the remaining balance after x of number of years

Answer 1

`A\text{ . }y=10000-250x`

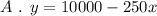
Step-by-step explanation

Step 1

find the slope of the line:

if you know 2 poitns(P1 and P2) of a lines, you can easily find the slope using:

`\begin{gathered} \text{slope}=m=(\Delta y)/(\Delta x)=(y_2-y_1)/(x_2-x_1) \\ \text{where} \\ P1(x_1,y_1) \\ P2(x_2,y_2) \end{gathered}`

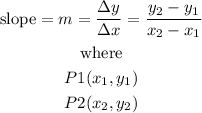
then, pick 2 points from the line in the graph

Let

P1(0,10000)

P2(40,0)

replace,

`\begin{gathered} m=(\Delta y)/(\Delta x)=(y_2-y_1)/(x_2-x_1)=(0-10000)/(40-0)=(-10000)/(40)=-250 \\ \text{slope}=-250 \end{gathered}`

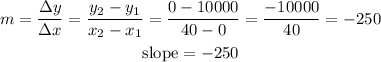
Step 2

Now, find the equation of the line,using:

`\begin{gathered} y-y_1=m(x-x_1) \\ \text{where} \\ P1(x_1,y_1) \end{gathered}`

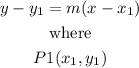
Let

P1(0,10000)

replace,

`\begin{gathered} y-y_1=m(x-x_1) \\ y-10000=-250(x-0) \\ y-10000=-250x \\ \text{add 10000 in both sides} \\ y-10000+10000=-250x+10000 \\ y=10000-250x \end{gathered}`

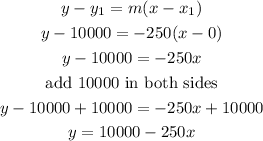
I hope this helps you